环境质量分析与评价方法主要有指数评价法、不确定评价法和智能评价模型等数十种之多(flores，2002; sanchez et al., 2007; bokar et al., 2004; li et al., 2011; cai et al., 2002; yang et al., 2007; kuo et al., 2004; dang et al., 2010; 邵磊等，2010)，这些方法和模型各有其特点(李祚泳等，2012).其中，不确定评价法虽然在环境质量分析评价过程中能在一定程度上反映系统的模糊性、灰色性和不相容性等特性，但评价函数的设计和计算工作量皆很大，且评价函数设计无规律可循，主观性较大;人工神经网络等智能评价法虽然在建模过程中模拟了人类大脑思维，但无明确的物理意义，且模型参数需要优化，编程较复杂，使用不便;传统的指数评价法虽然形式简洁、计算简单、结果直观，但评价结果有时难以反映真实污染状况.已有的各种环境质量分析评价公式、模型和方法均存在一个共同局限：可比性、普适性和通用性较差.环境质量分析评价过程实际上是将待评价样本与各级标准样本进行相似性比较，按其综合特征值大小进行聚类和识别.
万有引力存在于一切自然现象中.牛顿的万有引力定律描述为：任何两个物体之间存在相互作用的万有引力，其数值大小与它们的质量m1和m2的乘积成正比，与它们之间的距离r12的平方成反比.由于客观世界在某种意义上具有同一性，因此，已有学者将万有引力定律应用于图像识别和数据挖掘等问题的处理(顾丽敏等，2008;李卫平等，2006).受到上述研究的启迪，亦可认为：任何两个环境样本之间也存在类似万有引力的潜在的聚类相互作用的引力.因而只要将规范对称性(不变性)思想与万有引力定律相结合，在适当设定指标参照值和指标值的规范变换式及环境“参照级”样本的基础上，定义环境样本的“规范质量”及“规范坐标”的概念后，就可将万有引力定律引入环境质量评价、聚类和识别中，建立基于指标规范值的环境样本(或环境标准样本)与“参照级”样本之间的相互吸引的环境质量的万有引力指数公式(简称引力指数公式)，本文并将其应用于4类不同功能水体环境(地表水、地下水、海水和湖泊富营养化水体)质量及室内、外空气环境质量的实例分析评价.以期建立物理意义明确、科学合理、和谐统一、简洁直观、普适通用的环境质量评价指数公式，为环境保护、规划、污染防治技术和管理决策提供理论基础和技术手段.
2 环境指标的选取和指标参照值及指标值的规范变换式
依照国家制订的地表水环境质量标准(gb3838— 2002)、地下水环境质量标准(gb/14848—1993)、海水环境质量标准(gb3097—1997)、适用于我国湖库水体的富营养化标准及室外空气环境质量标准(gb3095—1996)和室内空气质量标准(gb/t18883—2002)，分别选取了4类水体的95项指标(其中，、地下水、海水和富营养化水体分别有24项、33项、23项和15项指标)和空气的29项指标(其中，室内空气15项指标和室外空气7项指标的年、日2种不同分级标准情形)作为水环境和空气环境的评价指标体系.
由于同类环境的不同指标的单位、量纲和同级标准数值都存在差异，因此，若直接依据各指标值描述环境质量不具有可比性和规范性，而采用“规范质量”表示环境质量较为方便.为此，对各指标j分别设定一个适当“参照值”cj0和相对于参照值cj0的规范变换式(1)~(7).各指标参照值cj0和指标值的规范变换式的设定原则为：通过对4类水体95项指标各级标准值的观察、分析、比较和提炼，使4类水体不同指标的同级标准值经规范变换后的同级标准规范值x′jk差异尽可能小，而不同标准之间的标准规范值差异尽可能大.这一过程需要对选择的cj0和规范变换式反复设置、试算和调整，直至满足要求为止.从而可以认为用规范值表示的4类水体的所有95项指标皆可与某个规范指标“等效”;类似，用规范值表示室内、外空气环境的29项指标也与某个规范指标“等效”.
式中，x′j 为指标j的规范值;xj为指标j的变换值，对4类水体和空气指标j设定的变换式分别如式(2)~式(7)所示.
a.地表水指标值变换式：
b.地下水指标值变换式：
c. 海水指标值变换式：
d.富营养化指标值变换式：
e.室外空气环境指标值变换式：
f.室内空气环境指标值变换式：
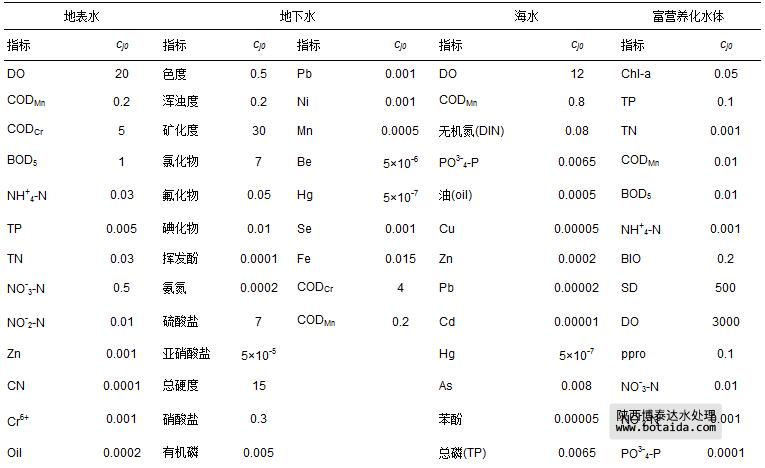
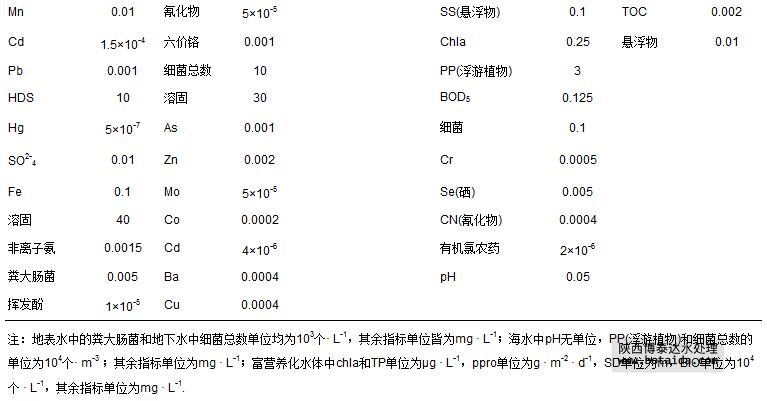
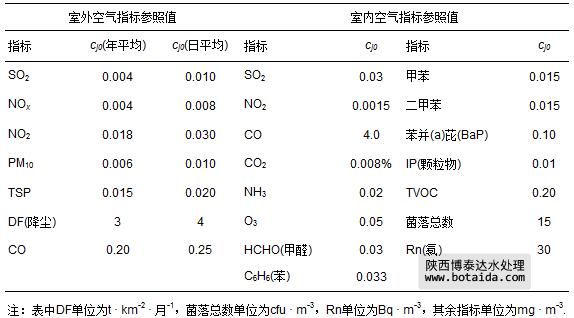
式(2)~(7)中，cj为指标j的实测值或标准值;cj0为设定的指标j的参照值，4类水体95项指标的参照值cj0和室内、外空气29项指标的参照值cj0分别如表 1和表 2所示.
表 1 4类水体95项指标的参照值
表 2 室内、外空气29项指标的参照值
3 基于指标规范值的环境质量的引力普适指数公式
3.1 环境质量引力普适指数公式
由于环境质量类别的有序性，因此，将万有引力定律用于描述环境质量时，需设定指标j的环境质量的“参照级”样本，此“参照级”样本的“规范质量”为mj∞.设“参照级”样本对环境各级标准样本或其他环境样本有潜在的聚类作用力，这种力可用引力公式来表示.依据万有引力定律，其引力大小与指标j的“参照级”样本的“规范质量”mj∞和指标j的样本的“规范质量”mj(或指标j的各级标准样本的“规范质量”mjk)的乘积成正比，与它们之间的距离平方成反比.若以横坐标表示样本的“规范质量”，并用指标j的规范值x′j表示，即mj= x′j，并规定任意指标j的“参照级”样本的“规范质量”mj∞皆等于“单位质量”，即有mj∞=x′j∞=1(j=1，2，…，m).x′j∞=1的意义为“参照级”样本的指标j的变换值xj∞足够大.此外，以纵坐标表示样本的“规范坐标”，并置“参照级”样本的“规范坐标”于纵坐标轴上r′j∞=1处.因此，指标j的“参照级”样本应位于x′j∞=1和r′j∞=1两条直线的交点p，而各级标准样本(或样本)应位于坐标原点o与点p的连线上。其余各级标准样本(或样本)的“规范坐标”可用r′jk(或r′j)表示.因此，各级标准样本(或样本)与“参照级”样本之间的“规范距离”应为1-r′jk(或1-r′j).然后依据万有引力原理，指标j的各级标准样本(或待评价样本)与“参照级”样本之间聚类相互吸引的环境质量引力指数公式为：
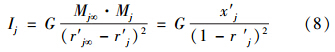
式中，mj和mj∞分别为指标j的样本“规范质量”和“参照级”样本“规范质量”;r′j为指标j的样本的“规范坐标”，显然r′j=x′j;g为环境质量引力常数，其取值大小只是为了控制指数ij的尺度范围，对评价结果无任何影响，为简单起见，在此取g=1.从而式(8)可表示为：
式中，x′j为指标j的规范值;分母中(1- x′j)为环境样本到设定的“参照级”样本的规范距离;ij为指标j的环境质量引力普适指数;x′b为对不同类型的环境设置的指标规范值的阈值.这是因为引力指数值ij近似呈规范值x′j的三次幂增大，为了限制过大的x′j对综合引力指数ij的影响，而设置了阈值xb.xb一般设置为某类环境最严重污染等级的所有指标规范值均值 ′j的1.1~1.3倍.因此，对水质指标分5级标准，其最严重污染的第5级标准的所有指标规范值均值 ′j5≈0.45，故取其均值的1.1倍，即取阈值x′b=0.5;而对空气指标分3级标准，其严重污染的第3级标准所有指标规范值均值 ′j3≈0.31，近似取其均值的1.3倍，即取阈值x′b=0.4.若污染物浓度的规范值x′j≥x′jb，则表明其对环境污染的危害程度已趋于饱和.从而得到4类水体的任一水质指标j的规范值x′j所表征水体样本与指标j的“参照级”样本之间的引力指数公式如式(10)所示.
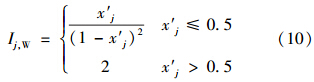
式中，x′j 为水质指标j的规范值.
类似地，任一空气指标的规范值所表征的室内、外空气环境样本与空气指标的“参照级”样本之间的引力指数公式如式(11)所示.
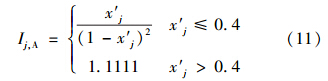
式中，x′j 为室内、外空气指标j的规范值.
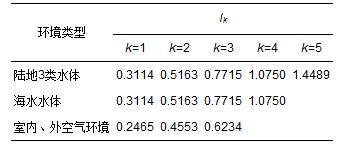
分别将4类水体95项指标的各级标准规范值x′jk代入式(10)，对第1~4级标准，将4类水体各级标准的所有95项指标的引力指数值求平均;对第5级标准，将地表水、地下水和富营养化3类水体的72项指标的引力指数值求平均.由于海水只分4级，因此，得到4类水体总体的引力普适指数值的分级标准值ik，具体如表 3所示.类似，将室内、外空气的29项指标的引力指数值求平均，得到室内、外空气质量的引力普适指数值的3级分级标准值ik，具体如表 3所示.而m项指标的水质引力综合指数公式和空气质量引力综合指数公式皆为：
表 3 4类水体及室内外空气环境的引力普适指数的分级标准值ik
式中，ij为由式(10)或式(11)计算得到的指标j的引力指数值;wj为指标j的归一化权值，即满足∑ m j=1 wj=1，它可以视实际问题需要，采用某种方法确定.一般情况下，只要各指标的规范值x′j差异不大，可视各指标为等权即可;但若最大指标规范值x′j，max与最小指标规范值x′j，min差异较大，则可采用如式(13)所示的对各指标规范值x′j的线性加权计算权值.
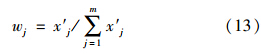
3.2 引力普适指数公式的可靠性分析
由于不同的环境指标的单位、量纲和数值大小往往都不相同，因此，无论采用何种方法作综合评价，都不可避免地必须对原始指标数据进行变换(比如极差归一化变换、标准差变换和本文采用的规范化变换等)，并将变换后的指标值代入模型、方法或公式进行分析、计算.因此，经多次变换后难免数据不失真，对公式的计算结果的可靠性有一定影响，此种影响程度可以通过对引力指数公式的灵敏度分析来确定.
由式(10)或式(11)，可得：
又由式(1)，可得：
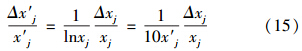
而变换式(2)~(7)皆可表示为如式(16)所示的一般形式.
式中，n为可正、可负的实数.由式(16)可得：
将式(17)、(15)代入式(14)得：
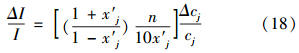
根据系统灵敏度定义，引力指数i对指标测值cj的灵敏度sc如式(19)所示.
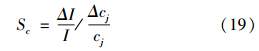
式中，
和
分别表示引力指数的相对误差和指标测值的相对误差.式(19)可写为：
比较式(18)和式(20)，可得如式(21)所示的灵敏度计算式.
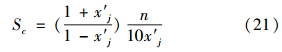
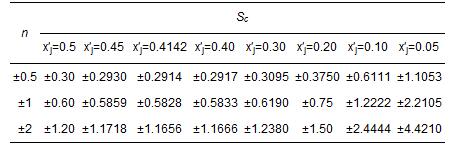
若n固定，将sc对x′j求导，并令s′c=0，得x′j=
-1≈0.4142时，sc有极小值0.5828n.由于变换式(2)~(7)中，对多数指标只取n=±2、±1、±0.5.而公式(10)和式(11)中，x′j 取值范围为x′j∈[0，0.5](对水体)，x′j∈[0，0.4](对空气).当n为上述值时，x′j 分别取为如表 4所示值时，由式(21)计算得灵敏度sc值如表 4所示.
表 4 相应于不同规范值x′j 的引力指数i对于指标监测数据cj的灵敏度sc
从表 4可见，当变换式的参数n∈[-1，1]时，其各级标准范围内模型灵敏度sc≤1，即引力指数i对指标测值cj的灵敏度sc为低灵敏度模型，表明实测值的相对误差不会被放大，反而被缩小;只有当n=±2的变换，才有可能被放大，但引力指数i的相对误差也仅是的1~2倍，故引力指数公式具有可靠性.
4 实例分析
为了验证式(10)和式(11)用于水体环境质量和空气环境质量评价的可行性和实用性，以下应用6个实例对式(10)和式(11)进行验证.
4.1 地表水水质评价实例分析
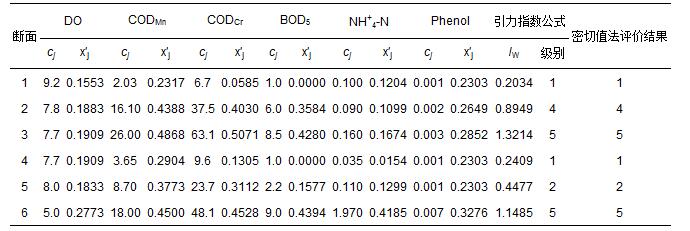
2008年图们江干流6个断面的6项地表水水质指标监测数据cj(唐立新等，2010)，以及由式(1)和式(2)计算得到的指标规范值x′j如表 5所示.对断面2和3，采用式(13)对引力指数值进行加权计算;其余断面在视指标为等权的情况下，用式(10)和式(12)计算得到各监测点水质引力综合指数值，并根据表 3中3类陆地水体的引力综合指数值的分级标准做出水质类别判断结果(表 5).表 5中还列出了参考文献(唐立新等，2010)中用密切值法作出的评价结果.可以看出，利用引力普适指数公式和用密切值法对6个断面水质做出的评价结果，完全一致.
表 5 图们江各断面水质指标监测数据cj(mg · l-1)及规范值 x′j和评价结果
4.2 地下水水质评价实例分析
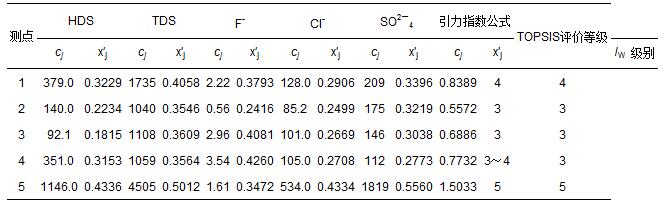
丰县5个监测点的5项地下水指标监测数据cj(刘洪等，2009)，以及由式(1)和式(3)计算得到的指标规范值x′j如表 6所示.在视各指标为等权情况下，用式(10)和式(12)计算得到各监测点水质引力综合指数的指数值，并根据表 3中3类陆地水体的综合指数值分级标准做出水质类别判断结果(表 6).表中还列出文献(刘洪等，2009)中用多属性决策分析法(topsis)做出的评价结果，可以看出，2种方法做出的评价结果完全一致.
表 6 丰县5个地下水监测点的指标监测数据cj(mg · l-1)及其规范值 x′j和评价结果
4.3 海水水质评价实例分析
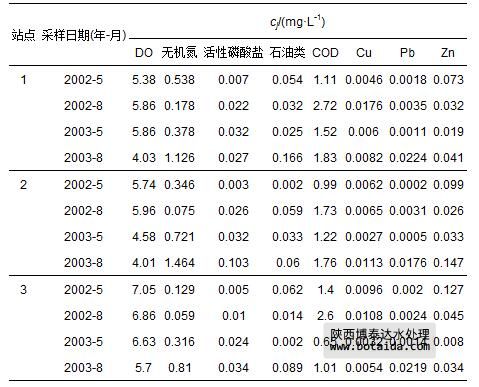
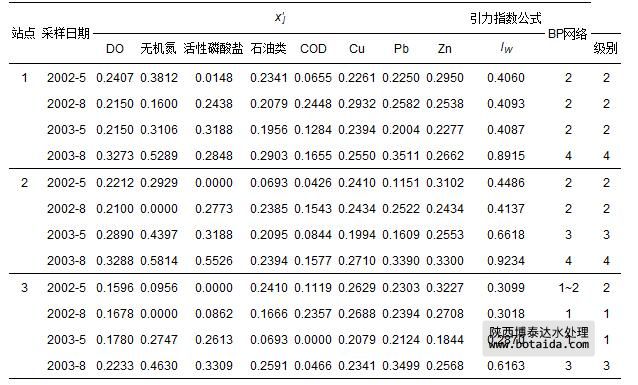
珠江口2002—2003年3个站点8项海水指标监测数据cj(李占东等，2005)如表 7所示.由式(1)和式(4)计算出的指标规范值x′j如表 8所示.由于站点1的2003-8和站点2的2002-5，2002-8和2003-5样本不同指标的规范值x′j相差较大，因而需用式(13)对引力指数值进行加权计算外.其余日期采样点则视各指标为等权，再用式(10)和式(12)计算得到各站点海水水质引力综合指数值，并根据表 3中海水水质引力指数分级标准做出评价结果(表 8).表中还列出文献(李占东等，2005)中用bp人工神经网络评价法做出的评价结果.可以看出，全部12个样本2种方法的评价级别完全一致.
表 7 珠江口2002—2003年3个站点水质指标监测数据cj
表 8 珠江口2002—2003年3个站点水质指标规范值 x′j和评价结果
4.4 湖库富营养化评价实例分析
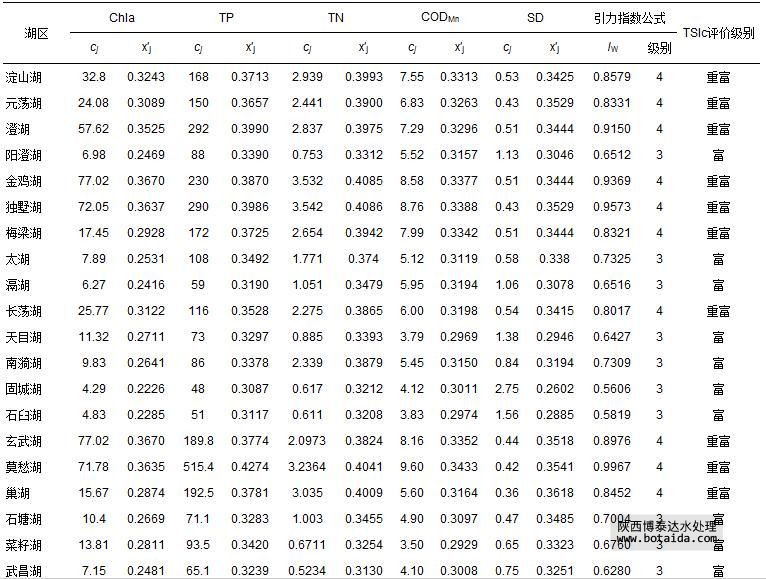
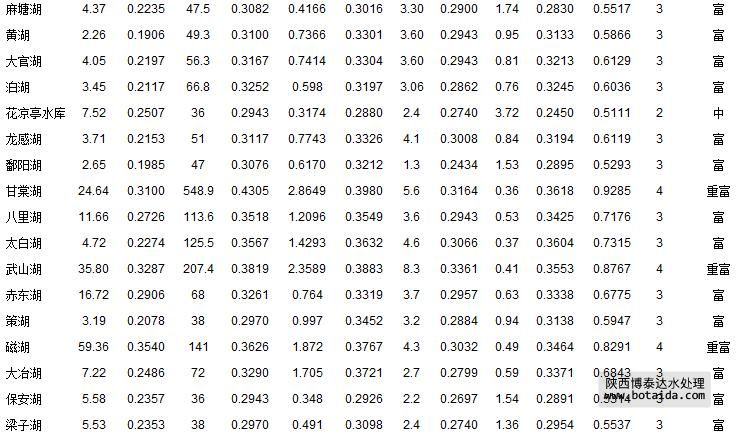
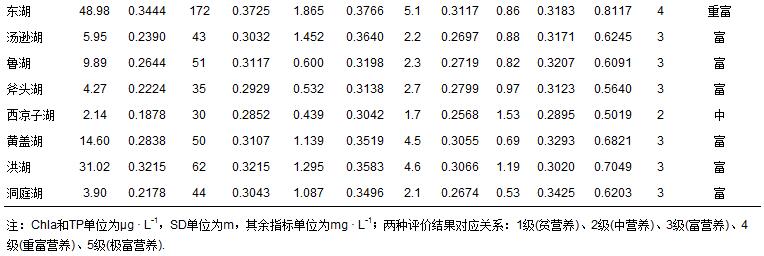
长江中下游45个湖泊的5项富营养化指标监测值cj(李祚泳等，2010)，以及由式(1)和式(5)计算出的指标规范值x′j如表 9所示.在视各指标为等权情况下，用式(10)和式(12)计算出引力综合指数的指数值，并根据表 3中3类水体的综合指数值分级标准作出的水质类别判断结果(表 9).表中还列出文献(李祚泳等，2010)用营养状态指数公式tsic作出的评价结果.可以看出，2种方法作出的评价结果完全一致.
表 9 长江中下游45个湖泊富营养化指标监测数据cj及其规范值 x′j和引力指数公式评价结果
4.5 室外空气环境质量评价实例分析
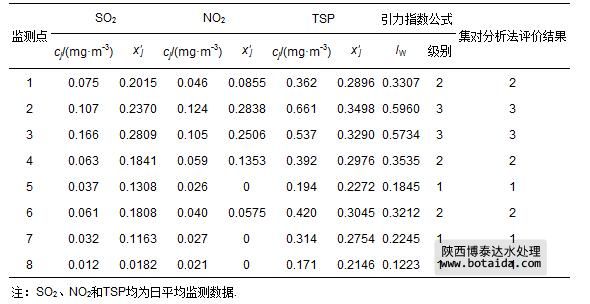
武汉市不同测点的空气指标日平均浓度监测数据cj(郭绍英等，2009)，以及由式(1)和式(6)计算出的指标规范值x′j如表 10所示.在视各指标为等权的情况下，将表 10中的3项指标规范值x′j分别代入式(11)和式(12)所示的引力指数公式，计算得到武汉市各测点空气质量引力综合指数值，并根据表 3中空气环境质量综合指数值分级标准作出的判断结果(表 10).表中还列出了参考文献(郭绍英等，2009)中用集对分析法作出的评价结果.可以看出，引力指数公式评价结果与集对分析评价结果完全一致.
表 10 武汉市不同测点空气质量监测数据cj及其规范值x′j和评价结果
4.6 室内空气环境质量评价实例分析
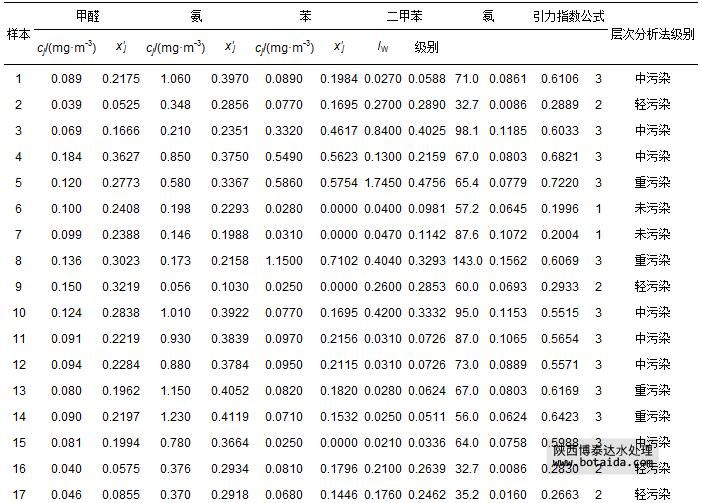
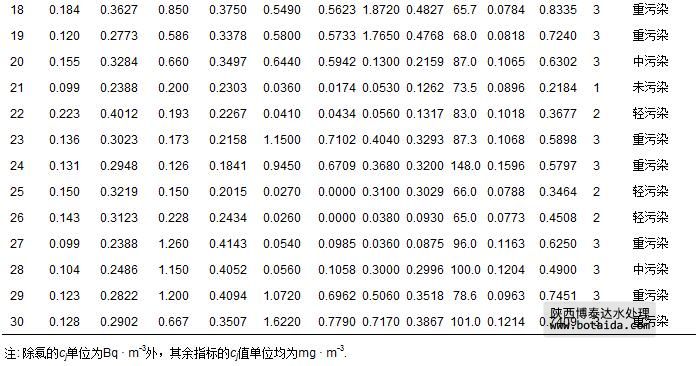
2002年11—12月长春市30个室内样本5项指标监测数据cj(汤红岩等，2005)，以及由式(1)和式(7)计算出的指标规范值x′j如表 11所示.由于样本1、11～15、26和27的不同指标计算得到的规范值相差较大，因此，在用式(12)计算引力综合指数时，需用式(13)对引力指数值进行加权计算，其余22个样本的指标视作等权，计算得到各样本引力综合指数值，并根据表 3中空气环境质量引力指数分级标准做出评价结果(表 11).表中还列出文献(汤红岩等，2005)中用层次分析评价法做出的评价结果.由于文献(汤红岩等，2005)中的层次分析评价法将室内空气污染划分为清洁(1*级)、未污染(2*级)、轻污染(3*级)、中污染(4*级)和重污染(5*级)等5级;而本文引力指数法将其划分为1级、2级、3级.二者对应关系为：(1*级清洁、2*级未污染)对应1级，(3*级轻污染)对应2级，(4*级中污染、5*级重污染)对应3级.由表 11可以看出，二种方法评价结果完全一致.
表 11 长春市30个室内样本监测数据cj及其规范值 x′j和评价结果
5 结论
基于“万有引力”原理和“规范变换”思想的水环境质量及空气环境质量的引力普适指数公式，物理意义明确，理论依据充分，对用规范值表示的4类水体任意水质指标和室内、外空气指标皆普适、通用.对于除表 1中4类水体的95项指标或表 2中室内、外空气的29项指标以外的其他水质指标和空气指标，只要能适当设定其参照值和指标值的规范变换式，使由规范变换式计算出的各级标准的规范值在表 1或表 2中指标的同级标准规范值变化范围内，则水环境或空气环境质量的引力指数公式(10)和公式(11)及表 3中给出的引力普适综合指数分级标准对这些指标同样适用.因此，环境质量引力指数公式具有更广泛意义的普适性.通过多个实例验证了环境质量引力指数公式的合理性、实用性和可行性，从而为环境质量评价提供了一种新方法.同时，本文提出的“规范质量”、“规范坐标”，“规范指标”，“等效指标”等新概念及环境质量规范变换思想、方法和引力普适指数公式易于拓广用于生态环境、水资源的可持续利用、水资源承载力、水安全和可持续发展等相关学科和领域的研究.